题目描述: 数字序列定义如下: f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) % 7. 现在给你A,B和n(1 <= A,B <= 1000, 1 <= n <= 1000000000),请你计算f(n)的值。
示例: 输入: A = 1 B = 1 n = 3 输出: 2
分析:
因为 1 <= n <= 1000000000, 所以如果使用传统的数组模拟方式,我们可能会超时,所以我们需要更加优秀的办法。
矩阵快速幂 就是用来解决这种问题的。我们需要了解两个 基础知识点: 矩阵乘法 和 快速幂
这里给出这两个知识点的简单描述。
矩阵乘法
一个 2 行 3列的矩阵,乘以一个 3 行 2列的矩阵,大小为 2 行 2 列。
n 行 m 列的矩阵乘以 m 行 k 列的矩阵,结果为 n 行 k 列的矩阵。
[2: 3] * [3 : 2] = [2:2]
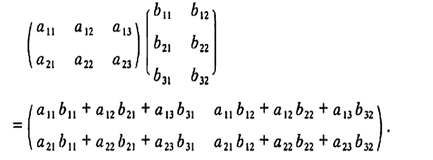
快速幂
\[A = a^5 = a^{101} = a^({2^2*1} + 2^1*0 + 2^0*1) = (a^{2^2} * 1) * (a^{2^1} * 0) * (a^{2^0} * 1)\]矩阵乘法和快速幂的实现见代码。
因为 f(n) = A*f(n-1) + B*f(n-2), f(n-1) = f(n-1) 所以见下:
\(\begin{bmatrix} f(n) \\ f(n-1) \end{bmatrix}\quad = \begin{bmatrix} A & B \\ 1 & 0 \end{bmatrix}\quad * \begin{bmatrix} f(n-1) \\ f(n-2) \end{bmatrix}\quad\) 所以: \(\begin{bmatrix} f(6) \\ f(5) \end{bmatrix}\quad = (\begin{bmatrix} A & B \\ 1 & 0 \end{bmatrix}\quad)^4 * \begin{bmatrix} f(2) \\ f(1) \end{bmatrix}\quad\)
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 矩阵乘法
def matrix_mul(mx_1, mx_2):
n, m = 2, 2
new_mx = [[0 for i in range(n)] for j in range(m)]
for i in range(n):
for j in range(m):
ans = 0
for k in range(m):
ans += mx_1[i][k] * mx_2[k][j]
# 注意取 余数
new_mx[i][j] = ans % 7
return new_mx
# 快速幂
def powful_matrix(mx, n):
res = [[1, 0],[0, 1]]
while n:
if n & 1:
res = matrix_mul(res, mx)
mx = matrix_mul(mx, mx)
n = n >> 1
return res
res_mx = powful_matrix([[A,B],[1, 0]],n-2)
ans = sum(res_mx[0]) % 7
print(ans)